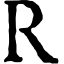1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
|
---
title: "An Introduction to Binarisation"
date: 2019-02-11
draft: true
categories: [binarisation, preprocessing, image manipulation]
---
Binarisation is the process of turning a colour or grayscale image into
a black and white image. It's called binarisation as once you're done,
each pixel will either be white (0) or black (1), a binary option.
Binarisation is necessary for various types of image analysis, as it
makes various image manipulation tasks much more straightforward. OCR is
one such process, and all major OCR engines today work on binarised
images.
Binarisation sounds pretty straightforward, and in the ideal case it is.
You can pick a number, and go through each pixel in the image, checking
if the pixel is lighter than the number, and if so declaring it to be
white, otherwise black.

The first issue with this is deciding what number to pick to determine
whether a pixel is white or black. This number is called the threshold,
and the whole process of binarisation can also called thresholding, as
it's so fundamental to the binarising process. Picking a threshold that
is too high will result in too few pixels being marked as black, which
in the case of OCR means losing parts of characters, which will make it
harder for an OCR engine to correctly recognise text. Picking a
threshold that is too low will result in too many pixels being marked as
black, which for OCR means that various non-text noise will be included
and considered by the OCR engine, again reducing accuracy.

If all page images were printed exactly the same way, and scanned the
same way, we could probably get away with just picking an appropriate
threshold number for everything. However sadly that is not the case, and
the variances can be significantly greater for historical documents.
There are various algorithms to find an appropriate threshold number for
a given page. A particularly well-known and reasonable one is called the
[Otsu algorithm](https://en.wikipedia.org/wiki/Otsu%27s_method). This
works by splitting the pixels in the image into two classes, one for
background and one for foreground, with the threshold calculated to
minimise the "spread" of both classes. Spread here means how much
variation in pixel intensity there is, so by trying to minimise the
spread for each class, the threshold aims to find two clusters of
similar pixel intensities, one being a common background, the other a
common foreground.
Otsu's algorithm works well for well printed material, on good paper,
which has been well scanned, as the brightness of the background and
foreground pixels is consistent.
However, even with the most perfectly chosen threshold number, there
are certain cases that no global threshold binarisation can do a good
job at. Pages which been scanned with have uneven lighting do badly,
as the background brightness may be quite different for one corner of
a page than another. Global threshold binarisation can also have
problems with paper or ink inconsistencies, such as blemishes,
splotches or page grain, as they may well have parts which are darker
than the global threshold.
{{< figure src="example-03.png" caption="Example of an image that can't be satisfyingly binarised using any global threshold." >}}
<!-- TODO: image demonstrating global thresholding failing on bad lighting -->
Both of these criticisms could be addressed by using an algorithm that
could alter the threshold according to the conditions of the region on
the page. That will be covered in the next blog post<!--,
[Adaptive Binarisation](/posts/adaptive-binarisation)-->.
|